逆正接関数(アークタンジェント) : 数学
正接関数(タンジェント)の逆関数である逆正接関数（アークタンジェント)の覚書です。
y = tanθ ⇔ θ = tan-1y -π/2 ≤ tan-1y ≤ π/2
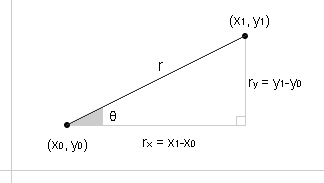
ある点(x0, y0)に対して半径(r)と弧度(θ)が与えられると1点(x1, y1)が定まる。
x1 = r×cosθ + x0 y1 = r×sinθ + y0逆に2点、(x0, y0)と(x1, y1)が与えられると(x0, y0)から(x1, y1)を中心とする半径(r)と弧度(θ)は下記のように求めることができる。
rx = x1-x0 ry = y1-y0
半径・・・ピタゴラスの定理で求める
r = √rx×rx+ry×ry
弧度・・・アークタンジェントで求める θ = tan-1(rx/ry)
ActionScript2.0の逆正接関数
»Math.atan, Math.atan2 : ActionScript
関連記事
コメント
コメントはまだありません。
コメントの投稿
改行と段落タグは自動で挿入されます。
メールアドレスは表示されません。
トラックバックURL
http://www.findxfine.com/science/math/277.html/trackback
