直線の媒介変数表示,内分点,外分点
直線の媒介変数表示の覚書です。直線(1次元)
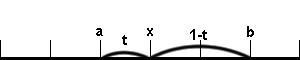
実数a,b(a<b)に対して、実数直線上の任意の点は媒介変数(実数)tを用いて下記のように表すことができる。
x = a + t(b-a) tは実数(媒介変数)上記は変形すると
x = (1-t)a + tb tは実数(媒介変数)
内分点・外分点
上記の式で媒介変数tが 0 ≤ t ≥ 1 ⇒ 内分点。 t ≤ 0, t ≥ 1 ⇒ 外分点。 媒介変数tを変化させることにa,bを通るすべての点を表すことができる。平面(2次元)
平面の2点(a1 ,a2),(b1, b2)を通る直線の内分点(x, y)を求める。
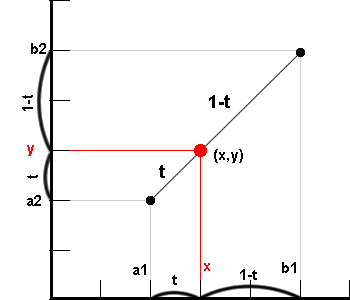
x= (1-t)a1+tb1 y= (1-t)a2+tb2
直線の方程式
平面上の2点(a1,a2),(b1,b2)を通る直線上の点を求める方程式。x = (1-t)a1+tb1 = a1+(b1-a1)t --(1) y = (1-t)a2+tb2 = a2+(b2-a2)t --(2)(1)をtについて解き、(2)へ代入する。
t = (x-a1)/(b1-a1)
y = a2+(b2-a2){(x-a1)/(b1-a1)}
y-a2 = {(b2-a2)/(b1-a1)}(x-a1) ---(3)
(3)で傾き(b2-a2)/(b1-a1)をmおく
y-a2 = m(x-a1) -- (4)(4)を変形して
y = mx-ma1+a2 --(5)-ma1+a2をkとおくと
y = mx + k※kはy切片になる
平行, 垂直
m, nの傾きを持つ2直線を考える。 2直線が平行 ⇔ m = n 2直線が垂直 ⇔ mn = -1 ⇒ n = -1/m関連記事
- 関連記事は見つかりませんでした。
検索ボックスからの検索もお試しください。
コメント
コメントはまだありません。
コメントの投稿
改行と段落タグは自動で挿入されます。
メールアドレスは表示されません。
トラックバックURL
http://www.findxfine.com/science/math/555.html/trackback
