合成関数の微分 : 数学
合成関数の微分
y = f(x), x = g(t)は微分可能な関数
dy/dt = f'(g(t))•g'(t)
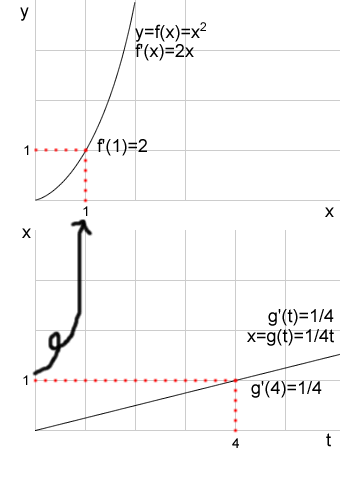
y=f(x)=x2 , x=g(t)=(1/4)t
dy/dx=2x, dx/dt=1/4
合成関数
y=z(t)=f(g(t))={(1/4)t}2
dy/dt = f'(g(t))×g'(t) = 2x×1/4 = 2·(1/4)t × 1/4 = (1/8)·t
dz(4)/dt = (1/8)×4 = 1/2
コメント
No comments yet.
コメントの投稿
改行と段落タグは自動で挿入されます。
メールアドレスは表示されません。