三角比・三角関数 : 数学

Tweet

Pocket

三角比・三角関数のメモ。

三角比

直角三角形の角度(Θ)に応じた2辺の比を三角比という。角度は度数で表す場合と弧度(ラジアン)で表す場合がある。
本記事では度数Θを弧度をθで表す。

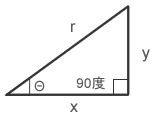
sinΘ = y/r			正弦
cosΘ = x/r			余弦
tanΘ = y/x			正接

sinΘ,cosΘ,tanΘは三角比という言葉のとおり直角三角形の辺の比を表す。
直角三角形の辺の比である三角比は、斜辺rの長さによって値が変わらず角度Θに応じて一意に決まる。
ある角度Θの直角三角形は、他の斜辺の長さが異なる全ての角度のΘ直角三角形と相似である。
相似な三角形の三角比は等しい。よって角度Θの三角比は斜辺の長さに関わらず一意に決まる。

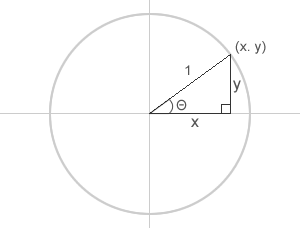
斜辺rが1の場合（r=1)

sinΘ = y;
cosΘ = x
tanΘ = y/x = sinΘ/cosΘ

斜辺1の三角比の余弦・正弦の値の組(x,y)は半径1(単位円)の円周上の点に対応する。

弧度(ラジアン:radian)

角度を表す方法は度数法と弧度法が有名である。
弧度法は、角度を半径1の円弧の長さで表す。
弧度の単位はradである。

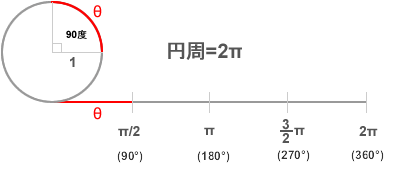
円周 : 2πr(rは半径)
単位円(r = 1) ⇒ 2πr = 2π
角度 ⇔ 弧度
·360度 = 2π ⇒ 360度/360 = 2π/360 ⇒ 1度 = π/180
1度を弧度で表すとπ/180(約0.017)
·360度 = 2π ⇒ 360度/2π = 1 ⇒ 180度/π = 1
1radを度数で表すと約57度

三角関数

半径1(単位円)の円弧(弧度)と三角比の関数を三角関数と呼ぶ。

x = cos(θ);
y = sin(θ);

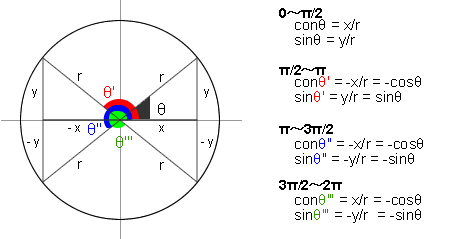
訂正 2009.01.25 上図 3π/2～2π
cosθ”’ = x/r = -cosθ ×
cosθ”’ = x/r = cosθ ○

sin,cos関数

三角関数の微分

sin' = cos
cos' = -sin

三角関数の冪級数展開

cosx =1 - x2/2! + x4/4! - x6/6! + ・・・
sinx = x - x3/3! + x5/5! - x7/7! + ・・・

逆関数

三角関数の逆関数を下記のように表す。

y = sinx ⇔ x = sin-1y (逆正弦関数)		※-π/2 ≤ sin-1y ≤ π/2
y = cosx ⇔ x = cos-1y (逆余弦関数)		※0 ≤ cos-1y ≤π
y = tanx ⇔ x = tan-1y (逆正接関数)		※-π/2 ≤ tan-1y ≤ π/2

※三角関数は周期関数のため、逆関数は多価関数となる。よって一般に値域を上記のように制限する。

極座標/媒介変数表示

半径rの円周上の点は角度θ(弧度)を用いて次のように表すことができる。

x = rcosθ
y = rsinθ

上記の式を極座標表示と呼ぶ。
また媒介変数表示でもある。