等加速度運動・等速度運動の公式 : 物理

Tweet

Pocket

等(加)速度運動の公式のメモ。

速度(v),
加速度(a)が与えらているときの時間(t)を変数とする距離(x)を表す。
等加速度運動の公式は時間t以外はベクトル量です。

等加速度運動の公式

時刻(t)を変数とする距離(x)の関数。

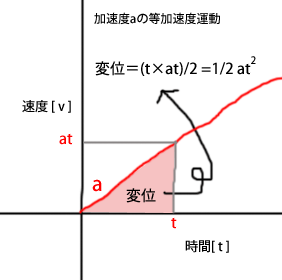
x = (1/2)at2+v0t		x:変位(m), a:加速度(m/s2), t:時間(s), v0:初速度(m/s)

時刻tを変数とする速度の関数

v = at+v0			v:速度(m/s), a:加速度(m/s2), t:時間(s), v0:初速度(m/s)

変位xを変数とする速度の関数

v2-v02=2ax	x:変位, a:加速度, v0:初速度

速度の公式を変形 t = (v-v0)/a
変位の公式に代入 x = (1/2)a(v-v0/a)2+v0(v-v0)/a
2x = (v-v0)2/a + 2(vv0-v02)/a
2ax =(v-v0)2 + 2vv0 + 2v02
2ax =(v-v0)2 + 2vv0 - 2v02 // コメント欄よりご指摘をいただき修正(2011.06.08)
2ax = v2 - v02

変位, 加速度, 初速度が与えられると、速度vを求めることができる。

等速度運動

加速度aが0の場合は等速度運動になる。

位置 : x = v0t			x:変位, t:時間, v0:初速度
速度 : v = v0			v:速度, v0:初速度

ActionScriptのサンプル

»onEnterFrameを使った等加速度運動・等速度運動 : Actionscript