回転行列 : 数学

投稿日 : 2008年5月7日 | 更新日 : 2010年11月17日 前のページへ戻る

回転行列のメモ。

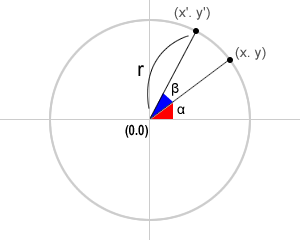
中心(0, 0)・半径rの円を考える。

2次の回転行列

原点(0,0)を中心に座標(x,y)に対して角度βだけ回転した得られる座標(x’,y’)は下記の式により求めることができる。

x' = cosβ·x - sinβ·y
y' = sinβ·x + cosβ·y

行列を使って表す。

[x'] = [cosβ -sinβ][x]
[y'] = [sinβ  cosβ][y]

係数行列を回転行列と呼ぶ。

[cosβ -sinβ]
[sinβ  cosβ]

同様に-β回転させる回転行列は次のようになる。

[cosβ  sinβ]
[-sinβ  cosβ]

導出方法

x = rcosα,y = rsinα ---(1)

加法定理
cos(α+β) = cosαcosβ - sinαsinβ ---(2)
sin(α+β) = sinαcosβ + cosαsinβ ---(2')

x' = rcos(α+β)
y' = rsin(α+β)

(2),(2')より
x'= r(cosαcosβ - sinαsinβ)
y'= r(sinαcosβ + cosαsinβ)

x' = rcosαcosβ  - rsinαsinβ
y' = rsinαcosβ + rcosαsinβ

(1)より
x' = xcosβ  - ysinβ
y' = ycosβ + xsinβ = xsinβ + ycosβ

3次元の回転

3次元の回転は、回転軸に応じて3種類ある。 回転軸の座標が固定されるため、2次元の回転と同じ行列が使える。

[cosβ -sinβ]
[sinβ  cosβ]

X軸に沿ったに回転行列

y' = ycosβ - zsinβ
z' = ysinβ + zcosβ

Y軸に沿った回転行列

z' = zcosβ - xsinβ
x' = zsinβ + xcosβ

Z軸に沿った回転行列

Z軸の回転は2次元(XY平面)の回転に対応

x' = xcosβ - ysinβ
y' = xsinβ + ycosβ

ActionScritのサンプル

»三角関数 回転行列を用いた円運動 : ActionScript

数学 | 固定リンク | Comments (0)

関連記事

関連記事は見つかりませんでした。
検索ボックスからの検索もお試しください。

このページの上へ移動

このページの上へ