3D基本事項(1点/0点透視法) : ActionScript -3D-

Tweet

Pocket

ActionScriptで3Dを表現するための覚書(AS2)。

3DをActionScriptで表現するには3次元である3D空間座標を2次元であるステージ(スクリーン)座標へ変換(投影,射影)する。
以下、変換を投影と呼ぶ。

投影方法の分類

• 遠近法(本記事では1点透視法) ・・・　本記事では遠近法を考える
• 射影関数

投影の流れ

1. 3次元3D空間座標を求める
2. 投影(遠近法や射影関数)により2次元ステージ座標を取得して表示

遠近法(1点透視法)

1点遠近法の原則

• 遠いほど小さく表示
• 近いものを手前に表示
• 遠くなるにつれて消失点に収束

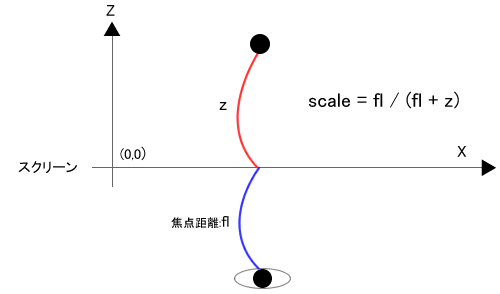
3D空間のz座標を用いて、3D空間を2次元へ投影する際の基準となる拡大率(scale)を求める。

scale = fl / (fl + z)
0 ≤ scale ≤ 1
z = 0 ⇒ scale = 1
z ≤ z' ⇒ scale  ≥ scale'
z → ∞ ⇒ scale = 0

遠近法の3次元空間原点(0, 0, 0)はステージ座標(0, 0, スクリーン位置)になる。
消失点とは3D空間のz座標が無限大になった際の物体の位置(消失点は空間内で共通して1つ)。

1点遠近法を用いて投影

焦点 fl
3次元空間座標(x_3d, y_3d, z_3d)
2次元空間座標(x_2d, y_2d)
消失点 vpx, vpy

// 拡大率
scale = fl / (fl + z3d)
// 2次元ステージ座標の取得
x2d = (x3d - vpx)*scale + vpx
y2d = (y3d - vpy)*scale + vpy
// サイズの変更
_xscale = _yscale = scale * 100;

0点透視法

曲線を投影する場合は消失点がない。そのため、1点透視法が使えない。
この場合は1点透視法の原則の中で「遠くなるにつれて消失点に収束」を考えないで、単に遠くのものを小さく、近いものを手前に表示すれば良い。

(例) 円運動

x3d = 中心X + 半径X×cosθ
y3d  = 中心Y + 半径Y×sinθ
z3d = 半径Z×sin;
var scale = fl/(fl+z3d);
x2d = x3d
y2d = y3d
_xscale = _yscale = 　scale;