曲線の描画2(curveTo) -媒介変数表示された曲線- : ActionScript

Tweet

Pocket

媒介変数表示された曲線の描画に関する覚書。

ActionScriptのCurveToで描画される曲線は2次ベジェ曲線。3点(始点,終点,コントロールポイント)を指定して描画する。
始点をa=(a_x,a_y),終点をb=(b_x,b_y)、コントロールポイントをc=(c_x,c_y)とすると下記のようになる。

MovieClip.MoveTo(ax,ay);
MovieClip.CurveTo(cx,cy, bx,by);

媒介変数表示された曲線を描画する際は、始点(a_x,a_y)と終点(b_x,b_y)を曲線上の点にとる。
コントロールポイント(c_x, c_y)は始点(a_x,a_y)、終点(b_x,b_y)それぞれにおける曲線の接線の交点をとる。

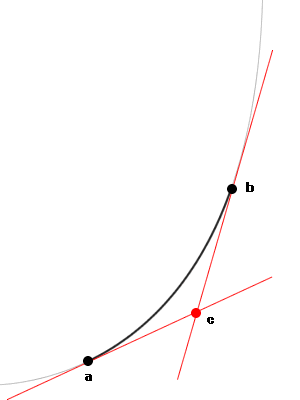
以下、媒介変数表示された曲線をcurveToを用いて描画する。
曲線を媒介変数表示することにより始点,終点における接線の交点を、行列式を用いて簡便に導出できる。

大まかな流れ

1) 曲線を媒介変数表示する。
2) 曲線上の始点,終点における接線の交点を求める。
3) curveToメソッドで描画する。

詳細な流れ

1) 媒介変数表示

2次関数の場合 : y = x²の場合。
媒介変数をtとする。

x = x(t) = t
y = y(t) = t2

円の場合 : (x-x₀)² + (y-y₀)² = r²。
媒介変数θとする。

x = x(θ) = rcosθ + x0
y = y(θ) = rsinθ + y0

2) 接線の交点

各点の始点(a_x,a_y)、終点(b_x,b_y)における接線の交点を求める。

媒介変数表示された曲線の接線の方程式は下記のとおり。
x(t)の微分をx'(t), y(t)の微分をy'(t)とすると

接線の方程式 : y -y(t) = {y'(t)/x'(t)}(x-x(t))
変形すると
y-y(t)/y'(t) = x-x(t)/x'(t)

始点(a_x,a_y), 終点(b_x,b_y)の2点における媒介変数をt=t_a, t=t_bとする。t_a,t_bにおける接線の方程式は

(y-y(ta))/y'(ta) = (x-x(ta))/x'(ta)
(y-y(tb))/y'(tb) = (x-x(tb))/x'(tb)

始点,終点の接線について連立方程式を解くことにより交点が導出できる。

始点(a_x,a_y)、終点(b_x,b_y)の接線の交点(c_x, c_y)は以下の行列式を用いることで簡便に求めることができる。

	| x'(ta)   x'(tb) |
	| detMa　 detMb    |
cx = 	-----------------------------------------------------------
	| x'(ta)  x'(tb) |
	| y'(ta)  y'(tb) |

	| y'(ta)  y'(tb) |
	| detNa   detNb   |
cy = 	-----------------------------------------------------------
	| y'(ta)  y'(tb) |
	| x'(ta)  x'(tb) |

detM =  | x(t)   x'(t) |
	| y(t)  y'(t) |

detN =  | y(t)  y'(t) |
	| x(t)   x'(t) |