内積 : 数学
内積の覚書
- 始点をO,終点がAのベクトルをOA(太字大文字)で表す(通常のOAは直線を表す)。
- ベクトルOAの終点Aの座標を(a1, a2)するとOAは座標(a1, a2)と同一視できる。a=(a1, a2)
- ベクトルaの大きさ/長さ/ノルムを|a|と表す。
- |a| = 1となるベクトルを単位ベクトルと呼ぶ。
- ベクトルa,bの内積をa·bと表す。
- 垂直なベクトルa,bをa⊥bと表す。
- BからOAにおろした垂線をBHとするとOHはbのa上への正射影ベクトル。
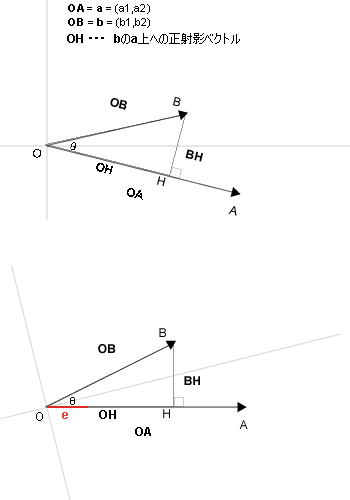
内積の演算規則 (1) a·(b+c) = a·b + a·c (2) 実数s,t, ベクトルa,b sa·tb = st(a·b) ベクトルa,bの内積 : |a||b|cosθ a·BH=0 a·BH=0 ⇔ a·HB=0 HB = OB - OH = b - OH 内積の演算規則(1)より a · (b - OH) = a·b-a·OH = 0 a·b = a·OH eをa方向の単位ベクトル(|e|=1)。θをベクトル間の角度とする。 a = |a|e OH = |b|cosθe 内積の演算規則(2),|e|=1 a·b = a·OH = (|a|e)·(|b|cosθe) = |a||b|cosθ(e·e) = |a||b|cosθ|e|2 = |a||b|cosθ 上記より cosθ = a·b / |a||b|
コメント
No comments yet.
コメントの投稿
改行と段落タグは自動で挿入されます。
メールアドレスは表示されません。