冪乗(累乗), 指数, 対数 : 数学
冪乗・指数・対数の覚書です。
冪乗(累乗)
aをn回掛けたものを冪乗(累乗)と呼びan(aのn乗)のように表す。
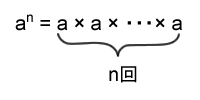
Wikipediaは冪乗を次のように説明している。
冪(べき、power, exponentiation)あるいは冪乗(べきじょう)、累乗(るいじょう) とは、ある一つの数同士を繰り返し掛け合わせるという操作のこと、あるいはそれによって得られる数のことである。
冪・冪乗・累乗は同じもの。冪が常用漢字・当用漢字に含まれていないために累乗が初等数学の教科書では使用されている。
指数
<
p>冪乗(累乗)anにおいてaを底、nを指数と呼ぶ。
a0 = 1
a1 = a とする。

指数法則
a>0, b>0, m, nを実数とする。 an·am = an+m an / am = an-m (an)m = anm (ab)n = anbn (a/b)n = an / bn
指数関数
指数を変数とする関数を指数関数と呼ぶ。
y = ax a>0かつa≠1
特に自然対数eを底とする指数関数を下記のように表すことがある。
eは(1+1/x)xの極限(lim x→∞)。
y = ex = exp(x)
指数関数の微分
(ax)' = axlogea (ex)' = ex (ekx)' = kekx 証明 z = kx y = f(z) = ez z = g(x) = kx (ekx)' = f'(z)g'(x) = ez·k = k·ekx
対数
(a>0かつa≠1について)an = Rを満たすときnをaを底とする真数Rの対数とよび下記のように表す。
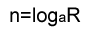
底を a = 10 とした対数を常用対数と呼ぶ。
底を a = eとした対数を自然対数とよぶ。eを自然対数の底と呼ぶ。
常用対数, 自然対数は底を省略して書かれることが多い。
底を2 とした対数は二進対数 (binary logarithm) といい、情報理論の分野で情報量などを表現するのに用いられることが多い。他の対数と区別するために “lg” という記号を用いることがある(対数 -Wikipedia –)。
対数の法則の覚書
loga(M×N) = logaM + logaN (例1) log2256 = log2(8×32) = log28 + log232 = 3 + 5 = 8 (例2) 以下、logeM = lnM ※eは自然対数の底(2.71828...) ln50 = ln(5×10) = ln5 + ln10 = 1.609... + 2.302... = 3.91...
底の変換公式
logax = logbx / logba
y = log1.052 = log102 / log101.05
となります。いま、近似的にlog101.05 = 0.02119, log102 = 0.3010であることを知っていたとすると
y = 14.20年
とおよその年数を求めることになります。
尾山 大輔ほか 「経済セミナー増刊 経済学で出る数学』 (pp57-58) 日本評論社
対数関数の微分
(logeX)' = 1/x (logaX)' = 1/xlogea
指数関数と対数関数
対数関数は指数関数の逆関数であり、y=xに対して対象。
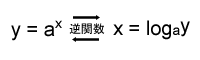
コメント
コメントの投稿
改行と段落タグは自動で挿入されます。
メールアドレスは表示されません。
本当によくよく解りました。本当にありがとうございました。
優之介
コメント by 優之介 — 2011-03-29 @ 4:02 PM
優之介さん。コメントありがとうございます。
とても励みになります。
コメント by findxfine — 2011-03-29 @ 5:35 PM