円 : 数学
円に関する覚書です。
円の方程式
原点を中心とする半径rの円の方程式。
x2 + y2 = r2 ---(1) {(x,y) | (x,y) ∈ x2 + y2 = r2}
中心(x0,y0)の場合の円の方程式。
(x - x0)2 + (y - y0)2 = r2 {(x,y) | (x,y) ∈ (x - x0)2 + (y - y0)2 = r2}
円の方程式はピタゴラスの定理から求めることができる。
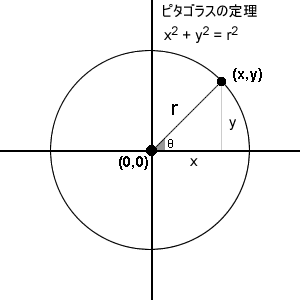
円を表す陰関数
(1)式を円の陰関数表示とも呼ぶ。
円の方程式/陰関数から2つの陽関数が得られる。
円を表す陽関数
x2 + y2 = r2 y = +√(r2 -x2) = -√(r2 -x2)
円を表すよう関数は変数xに対してyが2つ定まるため、関数※として扱うことができない。
そこで媒介変数(弧度)を利用することにより、媒介変数に対してx, yをそれぞれ一意に求める方法が使われる。
※関数をxに対して、yが一つ定まる関係とする。
媒介変数表示/パラメトリック表示
原点を中心とする半径(r)の円を考える。rを定数とすると、変数θ(弧度)対して、円の方程式を満たすx,yをそれぞれ下記の関数から求めることができる。
x = r·cosθ y = r·sinθ
円の接線
中心(0, 0), 半径rの円周上の点(a, b)の接線の方程式
円の方程式 : x2 + y2 = r2 接線の方程式 : ax + by = r2
※関係ない覚書
グラフの交点は連立方程式の解。
コメント
No comments yet.
コメントの投稿
改行と段落タグは自動で挿入されます。
メールアドレスは表示されません。